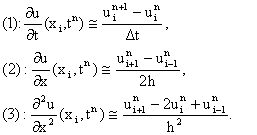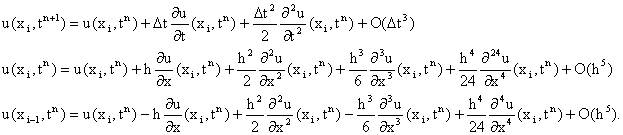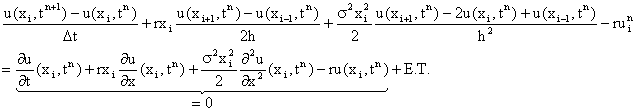La méthode des différences finies consiste à remplacer les dérivées apparaissant dans le problème continu par des différences divisées ou combinaisons de valeurs possibles de la fonction en un nombre fini de points discrets ou nœuds du maillage.

Discrétisation de l'EDP

On note u_iⁿ la valeur de la solution discrète approchant u(x_i,tⁿ).

Après la discrétisation du domaine, on effectue les approximations suivantes :

(1): différence finie progressive d'ordre 1,

(2) et (3): différence finie centrée d'ordre 2.

On obtient alors le schéma centré aux différences finies explicite en temps suivant :

où Dt<0.

Précision de l'edp

D'abord, on effectue les développements de Taylor suivants:

Puis, ces derniers sont injectés dans l'équation discrétisée:

où, l'erreur de troncature(E.T.) est:

Le schéma est consistant car E.T. tend vers 0 quand h tend vers 0 et quand Dt tend vers 0.