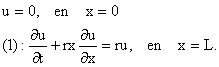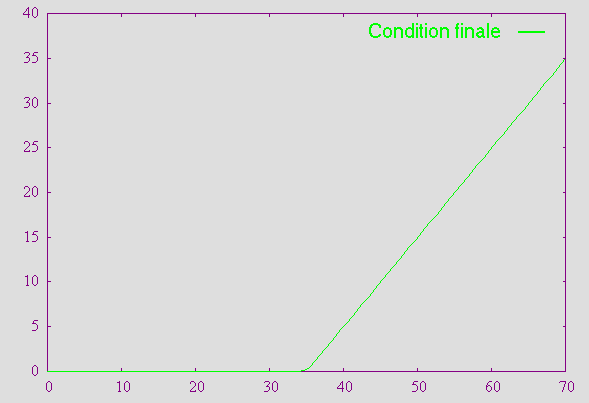
Condition finale

Le prix du call est dans le modèle de Black et Scholes, la somme d'argent dont on doit disposer initialement pour pouvoir suivre la stratégie de couverture et produire ainsi exactement la richesse max(0,x(t)-K) à l'échéance.

D'où, u(x,T)=max(0,x(t)-K).

remarque:

La condition finale peut-être plus compliquée. On peut considérer par exemple qu'il n'y aura de bénéfice que si la somme investie sur cette option rapporte plus que la somme déposée à la banque sur un compte rémunéré à un taux r.

Conditions aux limites

On limite le domaine de calcul à xÎ]0,L[ (afin de limiter le coût de calcul) et on introduit les conditions aux limites suivantes :

Or en x=L, u=x-K donc

D'où,

Pour x=0, il s'agit d'une condition de Dirichlet homogène.

Pour x=L, c'est une condition aux limites de Neumann (elle est compatible avec la condition finale).

Un autre choix possible de condition aux limites pour x=L est la solution exacte (obtenue de (1) et (2)) de :

On obtient alors :