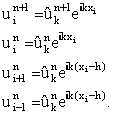Equation de transport homogène

Discrétisation par un schéma centré explicite

Précision

L'étude de la précision montre qu'il s'agit d'un schéma d'ordre 1 en temps et 2 en espace.

Stabilité

Pour étudier la stabilité d'un schéma aux différences finies, on utilise le plus souvent l'analyse de stabilité par Fourier. Dans cette méthode, on suppose que la solution du problème discret peut s'écrire sous la forme d' une série de Fourier. Les EDP étant linéaires, il suffit d'étudier le problème de stabilité pour un mode:

On remplace alors dans l'équation (A):

Comme

on obtient le facteur d'amplification du schéma numérique noté g_k suivant:

Le critère de Von Neumann assure que le schéma est stable si:

Or, |g_k|²>1 pour 0<kh<p et p<kh<2p.