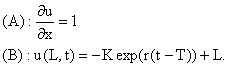|
||
|
|
Précédemment, 2 conditions aux limites ont été déduites à partir de l'équation :
Dans le but de montrer l'effet de ces conditions aux limites en x=L sur la solution du modèle de Black et Scholes, on modifiera le programme BS simplement en remplaçant la condition (A) par la condition (B) (il faut remplacer t-T par notre variable "temps-T").
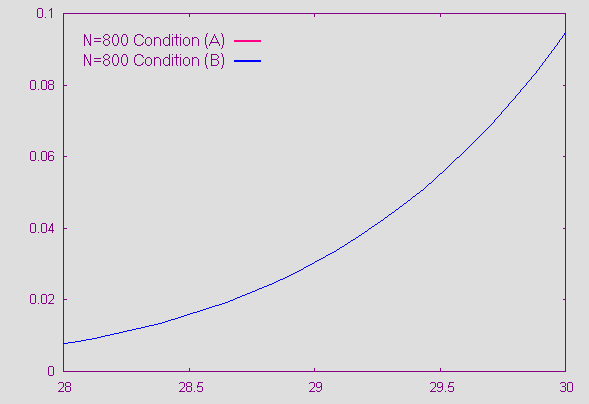
Effet du choix des conditions aux limites (A) et (B) en x=L sur la solution. Il semble qu'il n'y est pas d'écart selon le choix de la condition aux limites. Le problème vient du programme qui modifie seulement la solution de l'équation au point L lorsque l'on fait varier la condition limite.
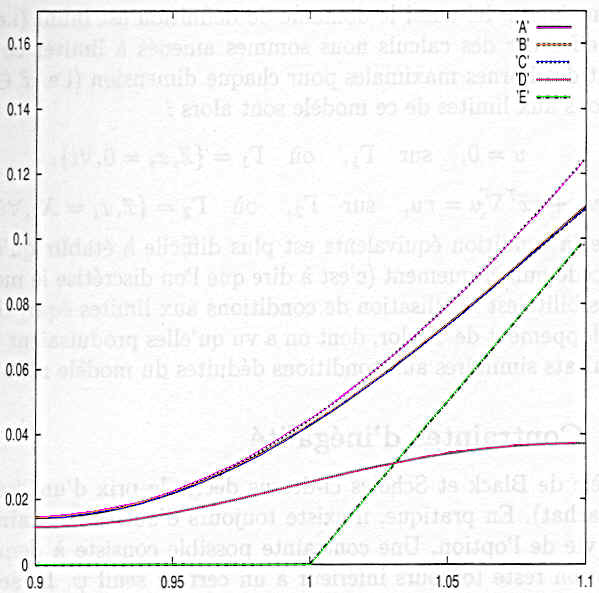
Effet du choix de la conditions aux limites en x=L au voisinage du prix de l'exercice (x/K=1) Ici, on ne s'intéresse qu'à l'effet sur nos 2 conditions limites précédentes. On voit nettement que le bon résultat est produit par la condition (B). On en conclue que la condition aux limites Mixte en x=L donne un meilleur résultat sur la solution du modèle de Black et Scholes. C'est cette condition qui servira lors de l'application à un exemple concret. |