Le modèle de Black et Scholes propose une équation qui ne dépend que d'un paramètre, non directement observable sur le marché, appelé volatilité s.

Elle caractérise l'incertitude du comportement: on remplace l'effet des fluctuations par une augmentation de la viscosité du système.

Afin d'étudier l'instabilité du modèle, le programme en BS est exécuté avec différentes valeurs (faibles) de s. (Dans ce contexte, on ne vérifie pas si ses valeurs ont un sens au niveau financier...)

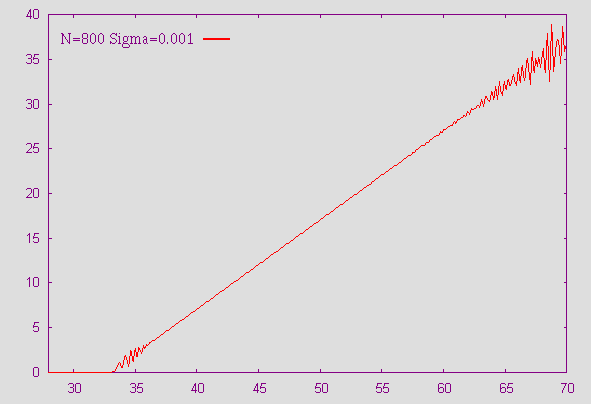
Etude de l'instabilité du modèle avec s=0.001

On obtient une nette instabilité pour s=0.001.

Cette instabilité du modèle était prévisible. En effet, lorsque l'on fait tendre s vers 0, le terme

tend vers 0. Et on se retrouve ainsi avec une équation aux dérivées partielles (edp) du type edp de transport, discrétisée par un schéma centré explicite mais qui est instable.

Dans ce cas,

peut alors être transformé en un schéma implicite centré inconditionnellement stable :

ou encore en un schéma explicite décentré (en amont car rx_i>0) stable sous la condition

On décide alors d'augmenter la précision du calcul en passant d'un programme en précision simple à un programme en précision double (BS). Il suffit pour cela de modifier dans le programme les variables "float" par des variables "double".

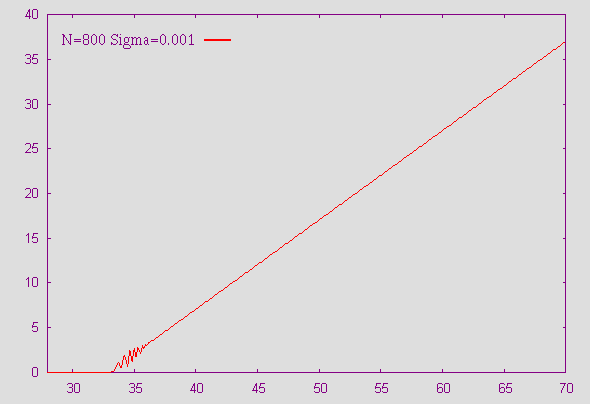
Etude de l'instabilité du modèle avec s=0.001

Pour une même valeur de s, on remarque qu'une instabilité persiste autour de X=35 (ce qui correspond à la valeur du prix d'exercice K). Par contre, il n'y a plus d'instabilité pour des grandes valeurs de X avec le programme en double précision. 

On en conclue que l'augmentation de la précision du calcul permet la diminution de l'instabilité. 

Pour l'application, nous utiliserons alors le programme en double précision.