 |
||
|
|
A l'aide d'un exemple concret (plus précisément un call européen), nous allons résoudre numériquement le modèle de Black et Scholes pour la prédiction du prix d'une option. Le programme BS1 en double précision fournit la solution u(x,0) de l'équation de Black et Scholes, c'est-à-dire le prix de l'option qu'il serait raisonnable de payer pour en principe ne pas avoir de perte.
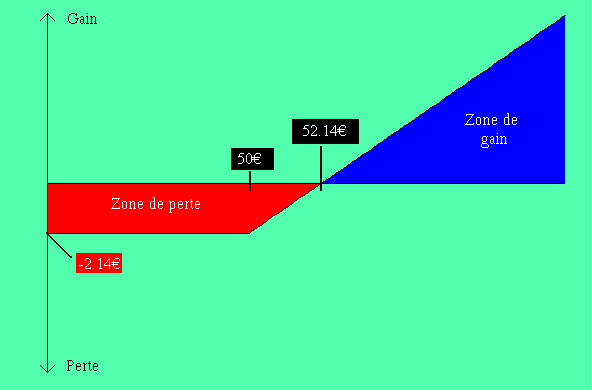
Extrait du journal Investir du 17 janvier 2003 Le 17 janvier, le call Renault 50€ à échéance du 20 mars 2003 cotait 2.14€ pour un cours du sous-jacent de 46.15€. A l'échéance, on exercera l'option si l'action Renault dépasse 50€. En tenant compte du prix d'achat, on sera gagnant (les frais de courtage étant supposés nuls) si le titre cote plus de 52.14€. Il s'agit d'une hausse modérée de 12% par rapport au cours initial de 46.15€. En revanche, on perdra notre mise si le cours est inférieur à 50€. On peut résumer tout ceci par le graphique suivant.
Achat d'un call Renault 50€ à échéance du 20 mars 2003 au cours de 2.14€ 
 |
Voici un extrait d'un journal
financier:
