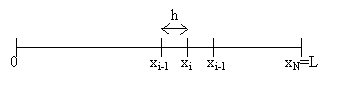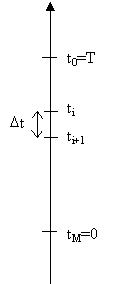Le problème de Black et Scholes est un problème exact (continu). Afin d'effectuer une résolution numérique, nous allons le discrétiser, c'est-à-dire le transformer en un problème approché (discret).

Discrétisation du domaine

Le maillage est l'opération qui consiste à discrétiser le domaine.

On procède à la discrétisation en espace et en temps.

Dans les 2 cas, on discrétise un intervalle continu de la forme [a,b] en un nombre fini de points afin de remplacer le problème continu par celui de la recherche de valeurs approchées u_iⁿ des solutions exactes u(x,t) aux points x_i du maillage et au temps discret tⁿ.

espace :

h est un pas régulier positif.

temps :

Pour la discrétisation, on a choisi un pas de temps régulier négatif.

La condition finale a donc lieu au point (x_i,0).

La deuxième étape de la discrétisation consiste à discrétiser l'edp par la méthode des différences finies.

Ainsi, connaissant la solution discrète en temps tⁿ (les u_iⁿ ), on obtient la solution discrète u_iⁿ⁺¹  au temps tⁿ⁺¹ par la relation :

La discrétisation du modèle permet alors d'obtenir le programme BS qui résout numériquement l'équation de Black et Scholes.

Dans la suite, les données suivantes seront utilisées lors de l'exécution du programme:

N=800

r=0.03

s=0.05

K=35

T=2