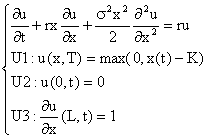 |
|
|
|
Pour obtenir des formules des prix des options, l'évolution des cours a été modélisé par Black et Scholes (*). Ce modèle conduit à une formule explicite pour le prix d'un call européen sur une action ne donnant pas de dividende et à une stratégie de gestion qui, dans le cadre du modèle, permet au vendeur de l'option de se couvrir parfaitement, c'est à dire d'éliminer totalement le risque. Soit C le prix d'un call européen dont le prix d'exercice est K. Le cadre est celui d'un marché comportant 2 actifs, un actif risqué (action) et un actif non risqué de rendement r définissant le taux d'intérêt (annuel) sans risque. On note T l'échéance (exprimée en mois), s la volatilité (supposée constante) et x(t) le prix de l'action à toute date 0£t£T.
où K>0, tÎ]0,T[ et xÎ]0,L[. U1,U2 et U3 sont respectivement la condition finale et les conditions limites. Il s'agit d'une équation parabolique rétrograde en temps pour le comportement de u. Pour
une explication plus précise de l'origine de l'équation... (*)F. Black et M. Scholes. The pricing of options and corporate liabilities. Journal of Political Economy. 1973, pp. 637-654. 
 |
Selon Black et Scholes, la valeur théorique d'une option d'achat u(x,t) est solution
de l'équation suivante :
